中華文明歷史悠久,中華文化博大精深,、源遠流長,,中國古代數(shù)學(xué)也一樣有著輝煌的成就。華羅庚先生說過,,中華民族是最擅長數(shù)學(xué)的,。作為微積分學(xué)的基礎(chǔ)的極限理論直到19世紀才得以完善,但是極限思想的萌芽可以追溯到大約兩千五百年前,,在中國和西方都展現(xiàn)出了極限的思想,。而我國是世界上最早產(chǎn)生極限思想和應(yīng)用極限思想的國家。
早在春秋戰(zhàn)國時代(公元前770——前221),,《莊子·天下篇》 中有這樣一句:“一尺之棰,,日取其半,萬世不竭”,。意思就是說:一尺長的一根木棒,,如果每天截下一半,永遠都取不完,,這樣的過程可以無限地進行下去,。另外,在《墨子·經(jīng)下》中有也有一句:“非半弗斫,,則不動,,說在端?!边@句話的意思是說,,一條線段從中點分為兩半,取其一半冉破成兩半,,仍取一半繼續(xù)分割,,直到不可分割時就只剩下一個點。這些體現(xiàn)出了古人對無限思想的認識,,蘊含了樸素的,、直觀的極限思想,。

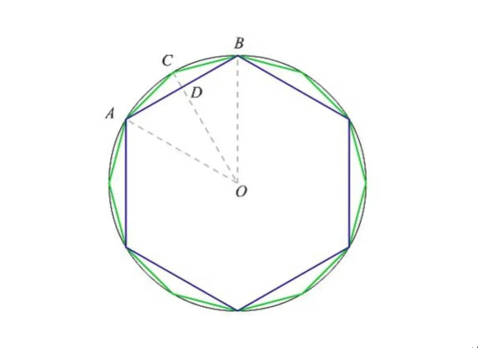
魏晉時期(公元3世紀),我國的數(shù)學(xué)家劉徽在《九章算術(shù)注》中寫到:“以六觚之一面乘半徑,,因而三之,,得十二觚之冪。若又割之,,次以十二觚之一面乘半徑,,因而六之,則得二十四觚之冪,。割之彌細,,所失彌少。割之又割,,以至于不可割,則與圓合體,,而無所失矣,。”這里“觚”是正多邊形,,“面”是正多邊形的邊,,“冪”是正多邊形的面積。劉徽的方法就是先做一個圓內(nèi)接正六邊形,,然后平分每組對邊的弧,,作出圓的內(nèi)接正十二邊形,同樣的方法繼續(xù)作圓的內(nèi)接正二十四邊形,、四十八邊形……正多邊形的邊數(shù)越多,,即所謂“割之彌細”,圓的面積與正多邊形的面積相差就越少,。當(dāng)分割次數(shù)無限增加,,也就是正多邊形的邊數(shù)無限增大時,正多邊形將與圓重合,。用我們今天的說法就是圓內(nèi)接正多邊形面積的極限即為圓面積,。這就是劉徽著名的割圓術(shù),割圓術(shù)是極限思想在幾何上的應(yīng)用,。

祖率在西方直到1573才由德國人奧托得到,,1625年發(fā)表于荷蘭工程師安托尼斯的著作中,歐洲稱之為安托尼斯率,。祖沖之的圓周率保持了千年之久,,直到 15 世紀才被阿拉伯?dāng)?shù)學(xué)家阿爾·卡西打破 , 計算到小數(shù)點后 17 位。

祖沖之和他的兒子祖暅編寫了一本名為《綴術(shù)》的專著,,這本書在唐代初期被選作國子監(jiān)算學(xué)館的教材之一,。據(jù)說《綴術(shù)》的內(nèi)容十分艱深,、是唐朝算學(xué)中最難的課本,所以習(xí)者寥寥,。在北宋元豐七年(1084年)時?便已經(jīng)失傳,,非常可惜,?!毒Y術(shù)》中有云:“緣冪勢既同,則積不容異”,。意思是說:如果兩個立方體的所有等髙的橫截面積全都相等,, 那么這兩個立方體的的體積一定是相同的。這正是“不可分量”思想的延續(xù),。這個原理我們稱之為“祖暅原理”,,在微積分里被西方稱為卡瓦列里(Cavalieri)原理。祖暅原理的發(fā)現(xiàn)比卡瓦列里原理早1000 多年,。 祖暅承襲了劉徽的思想,,利用祖暅原理求出“牟合方蓋”的體積,進而利用“牟合方蓋”求出了球體的體積,,解決了劉徽所遺留的問題,。

《綴術(shù)》代表了當(dāng)時數(shù)學(xué)的最高水平價值,但是由于已經(jīng)失傳,,我們無法得知其內(nèi)容,。有學(xué)者認為《綴術(shù)》中會蘊含極限思想,因為“綴” 本身字就有“連續(xù)”之含義,。
劉徽,、祖沖之都是我國歷史上杰出的科學(xué)家。他們的科學(xué)發(fā)現(xiàn)與創(chuàng)造是我國古代科技發(fā)展成就的重要代表之一,,他們的研究對于人類社會的發(fā)展做出了極 大的貢獻,,他們的卓越貢獻對世界都有著深刻的影響。
本文只是介紹了中國古代數(shù)學(xué)成就中關(guān)于極限思想的一小部分,,中國古代數(shù)學(xué)的成就遠遠不止于此,。在悠久的歷史長河中,我們有先進的科技文化,,有無數(shù)卓越的數(shù)學(xué)家,,我們曾是數(shù)學(xué)領(lǐng)域的領(lǐng)跑者。雖然今天,,在某些方面我們略有落后,,但是只要有信心、不放棄,、勇攀登,,相信我們必然會崛起,!
作者:殷紅燕;編輯:胡軍浩,;審核:李海濤,;上傳:劉鹍。


